Systemy rekomendacji - Jak działa cross selling w e-commerce?

Trudno sobie wyobrazić funkcjonowanie Internetu bez analizy zachowania użytkowników. To właśnie te zachowania stały się wspólnym mianownikiem dla wielu elementów warunkujących rozwój technologii, w tym także rynku e-commerce. Wykorzystywanie dostępnych danych w celu lepszego zrozumienia zwyczajów i preferencji użytkownika przez systemy informatyczne, jest jednym z flagowych przykładów zastosowania algorytmów rekomendujących.

Wstęp

Rosnący rynek e-commerce

Z dostępnych danych wynika, że globalny rynek e-commerce, uznawany jest wciąż jako niezupełnie nasycony. Według badań prowadzonych przez Główny Urząd Statystyczny, w Polsce dostęp do Internetu posiada 92,7 % przedsiębiorców z czego tylko 65,4 % z nich prowadzi własne strony internetowe. Prowadzenie sprzedaży w Internecie stało się ważnym filarem w procesie funkcjonowania i świadomości finansowej przedsiębiorców, co można zaobserwować po dynamicznym wzroście wartości tego rynku.

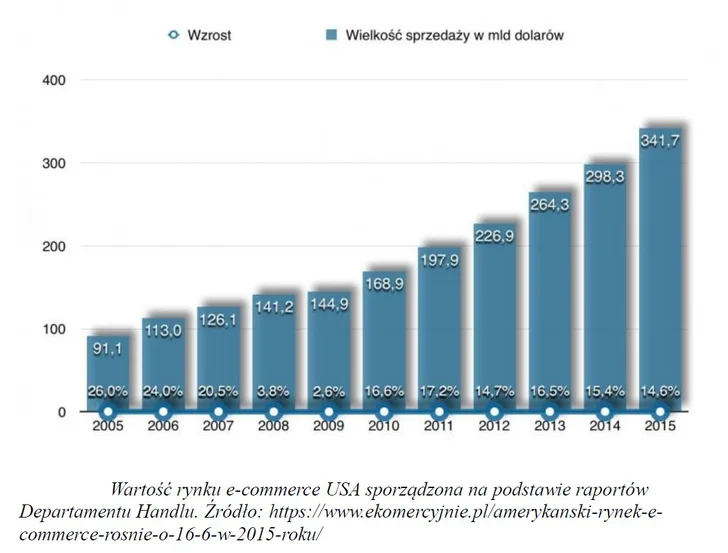
Wartość rynku e-commerce w USA

Coraz lepsze badanie potrzeb odwiedzających

Jednym z głównych czynników, który stoi za prezentowanym rozwojem jest rosnący popyt na usługi i produkty sprzedawane w sieci. Jednocześnie dla sprzedawców ważnym stało się dostarczenie klientowi takiego produktu, który stałby się dla niego atrakcyjny i tym samym skłaniał go do jego zakupu, przy możliwie jak najmniejszym koszcie pozyskania tego użytkownika.

W osiągnięciu tego celu pomaga zrozumienie oraz stałe reagowanie na potrzeby, zachowania i nawyki odwiedzających.

Model matematyczny

Generalnie problem występujący w systemach rekomendujących możemy sprowadzić do zadania regresji:

Dla każdego użytkownika 𝑼 = {𝑢1, 𝑢2, … } oraz produktu 𝑰 = {𝑖1, 𝑖2, … } znaleźć funkcję docelową oceny 𝑦(𝑢, 𝑖) produktu 𝒊 przez użytkownika 𝒖 taką, że 𝑦: 𝑈 × 𝐼 → R.

Jednocześnie mając podany zbiór wartości obserwacji wejściowych funkcji 𝑦(𝑢, 𝑖) dla podanego zbioru 𝑆 ⊂ 𝑈𝑥𝐼, zadaniem algorytmu jest predykcja 𝒚̂ oceny produktu przez nowego jak i dotychczasowego użytkownika.

Collective intelligence

W systemach o podanej wyżej charakterystyce bazujemy na założeniu, że podobni do siebie użytkownicy będą wykonywać podobne ruchy i podejmować podobne decyzje. W metodzie tej mierzymy więc „mądrość tłumu”, w literaturze często określanej także inteligencją zbiorową (ang. collective intelligence), poprzez wykorzystanie historycznych wzorców zachowań w serwisie.

Zadanie to staje się o tyle problematyczne, że opinia może być jawna (ang. explicite) lub niejawna (ang. implicite).

Do jawnych metod należą:

• oceny bezpośrednie produktu (np. w skali od 1 do 5 – popularne gwiazdki);
• polubienia (metoda wykorzystywana przez takie serwisy jak YouTube czy Facebook);
• sortowanie bądź rankingowanie ofert (np. w formie listy preferencji).

Do metod niejawnych najczęściej należą:

• fakt oglądania/przesłuchiwania danej oferty;
• czas spędzony na stronie;
• liczba i rodzaj słów kluczowych na których koncentrujemy naszą uwagę w stosunku do innych;
• komentarz;
• zakup produktu;
• skopiowanie adresu URL.

Systemy Information retrieval

Jeżeli natomiast rozpatrywalibyśmy systemy rekomendujące jako podklasę systemów Information retrieval (IR) , to możemy dokonać ich podziału na:

• User-based / Collaborative Filtering – przewidywanie (filtrowanie) w oparciu o zbieranie preferencji lub informacji o gustach innych użytkowników9 ;
• Content / Knowledge-based Filtering – przewidywanie (filtrowanie) w oparciu o szereg dyskretnych cech elementu10;
• Non – personalized – rekomendacja najpopularniejszych przedmiotów wszystkim użytkownikom11;
• Hybrid Systems – podejście hybrydowe, wykorzystujące wiele technik w celu osiągnięcia najlepszego rezultatu;
• Inne: Personalized Learning to Rank, Deep Learning, Context Aware Recommendation.

Normalizacja danych jest konieczna

Chciałbym podkreślić, że w systemach rekomendujących bardzo duży problem stanowi potrzeba odpowiedniej normalizacji analizowanych zmiennych.
W pewnym momencie może się okazać, że bagatelizując proces odpowiedniego przygotowania zbioru danych do jego analizy, otrzymamy zupełnie różne od zakładanych rezultaty.

Celem jest więc zmniejszenie wymiarowości problemu do jak najbardziej istotnych cech

O najprostszych mechanizmach normalizacji danych przygotuję osobny wpis.

Wykorzystywane miary podobieństwa

Miara podobieństwa jest wskaźnikiem tego, jak bardzo podobne są dwa porównywane ze sobą obiekty.

Miarą podobieństwa w kontekście eksploracji danych jest odległość między punktami reprezentującymi cechy obiektów. Jeśli ta odległość jest niewielka, stopień podobieństwa jest wysoki, duża odległość oznacza natomiast niski stopień podobieństwa.

Podobieństwo jest subiektywne oraz wysoce zależy od dziedziny i zastosowania. Na przykład dwa owoce są podobne ze względu na kolor, rozmiar lub smak.

Należy zachować ostrożność przy obliczaniu odległości między wartościami cech, które nie są ze sobą powiązane.

Względne wartości każdego elementu muszą zostać znormalizowane, gdyż jedna cecha może w końcu zdominować obliczanie odległości, powodując powstawanie błędnych relacji.

Odległość euklidesowa

Odległość euklidesowa jest najprostszą metodą pomiaru podobieństwa między poszczególnymi elementami w procesie odkrywania wiedzy z danych.

Formalnie rzecz biorąc miara ta jest odległością wyrażoną za pomocą linii prostej między dwoma punktami umieszczonymi w danej przestrzeni metrycznej:

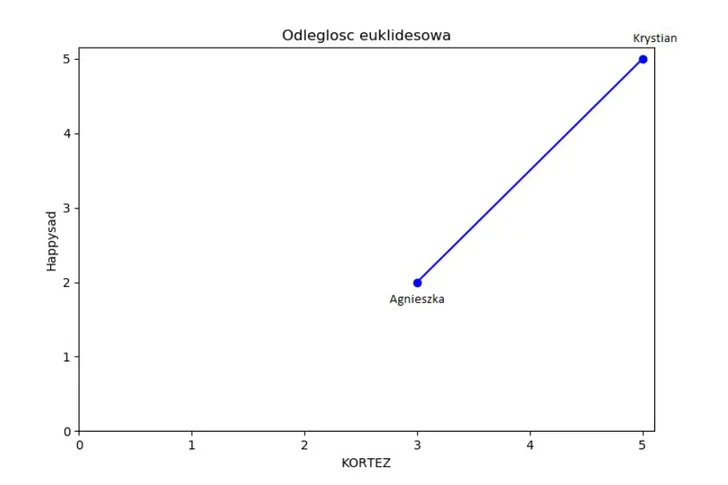
Odległość euklidesowa

Dana jest ona wzorem:

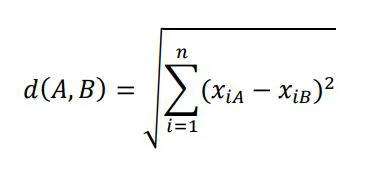
Odległość euklidesowa - wzór

gdzie:

𝑛 − wielkość rozpatrywanej przestrzeni

𝑥𝑖𝐴 − wartość punku 𝐴 w przestrzeni

𝑖 𝑥𝑖𝐵 − wartość punktu 𝐵 w przestrzeni R

W przestrzeni dwuwymiarowej, analizowanej na wykresie, wzór redukuje się do:

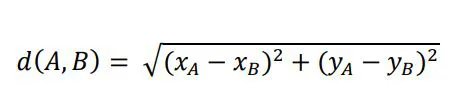
odleglosc euklidesowa wzor dla r2

przy czym:

𝑥𝐴 − 𝑤𝑎𝑟𝑡𝑜ść 𝑝𝑢𝑛𝑘𝑡𝑢 𝐴 𝑛𝑎 𝑜𝑠𝑖 𝑜𝑑𝑐𝑖ę𝑡𝑦𝑐ℎ,

𝑦𝐴 − 𝑤𝑎𝑟𝑡𝑜ść 𝑝𝑢𝑛𝑘𝑡𝑢 𝐴 𝑛𝑎 𝑜𝑠𝑖 𝑟𝑧ę𝑑𝑛𝑦𝑐ℎ,

𝑥𝐵 − 𝑤𝑎𝑟𝑡𝑜ść 𝑝𝑢𝑛𝑘𝑡𝑢 𝐵 𝑛𝑎 𝑜𝑠𝑖 𝑜𝑑𝑐𝑖ę𝑡𝑦𝑐ℎ,

𝑦𝐵 − 𝑤𝑎𝑟𝑡𝑜ść 𝑝𝑢𝑛𝑘𝑡𝑢 𝐵 𝑛𝑎 𝑜𝑠𝑖 𝑟𝑧ę𝑑𝑛𝑦𝑐ℎ.

Podstawiając przedstawione na wykresie punkty (3,2) oraz (5,5) do w/w wzoru otrzymamy pierwszą wartość podobieństwa pomiędzy użytkownikami 😋 :

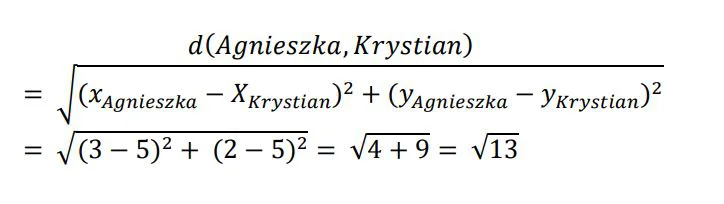
Odległość euklidesowa wynik

ciąg dalszy tego artykułu dostępny będzie już wkrótce :).